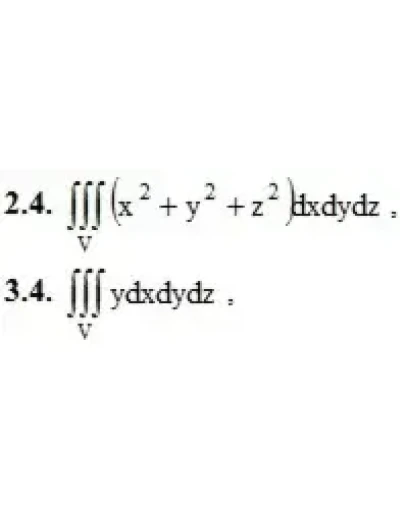1. Расставить пределы интегрирования в тройном интеграле если область V ограничена указанными поверхностями. Начертить область интегрирования
1.4. V: x = 3, y = x, y ≥ 0; z ≥ 0, z = 3x2 + y2
2. Вычислить данные тройные интегралы.
V: 0 ≤ x ≤ 3, −1 ≤ y ≤ 2, 0 ≤ z ≤ 2
3. Вычислить тройной интеграл с помощью цилиндрических или сферических координат.
, υ: x2 + y2 + z2 = 32, y2 = x2 + z2, y ≥ 0
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
4.4. z = y2, x ≥ 0, z ≥ 0, x + y = 2
1.4. V: x = 3, y = x, y ≥ 0; z ≥ 0, z = 3x2 + y2
2. Вычислить данные тройные интегралы.
V: 0 ≤ x ≤ 3, −1 ≤ y ≤ 2, 0 ≤ z ≤ 2
3. Вычислить тройной интеграл с помощью цилиндрических или сферических координат.
, υ: x2 + y2 + z2 = 32, y2 = x2 + z2, y ≥ 0
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
4.4. z = y2, x ≥ 0, z ≥ 0, x + y = 2