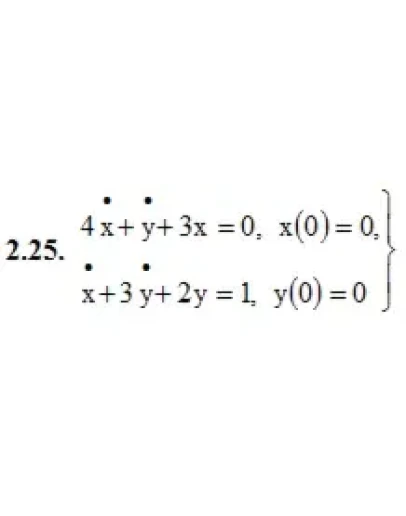1. Решить операторным методом линейное дифференциальное уравнение
αẍ + βẋ + γx = f(t), x(t0) = A, ẋ(t0) = B
Функцию f(t) и значения коэффициентов α, β, γ, t0, x(t0), ẋ(t0) взять из табл. 16.4
1.25. α = 1, β = −1, γ = 0, f(t) = t2, t0 = 0, x(t0) = 0, ẋ(t0) = −1
1.25. ẍ − ẋ = t2, x(0) = 0, ẋ(0) = −1
2. Решить операторным методом систему линейных дифференциальных уравнений
Функции f1(t), f2(t) и значения ak, bk, ck, dk (k=1, 2), A, B, x(0), y(0) взять из табл. 16.5
2.25. a1 = 4, b1 = 1, c1 = 3, d1 = 0, f1(t) = 0, a2 = 1, b2 = 3, c2 = 0, d2 = 2, f2(t) = 1, x(0) = 0, y(0)=0
αẍ + βẋ + γx = f(t), x(t0) = A, ẋ(t0) = B
Функцию f(t) и значения коэффициентов α, β, γ, t0, x(t0), ẋ(t0) взять из табл. 16.4
1.25. α = 1, β = −1, γ = 0, f(t) = t2, t0 = 0, x(t0) = 0, ẋ(t0) = −1
1.25. ẍ − ẋ = t2, x(0) = 0, ẋ(0) = −1
2. Решить операторным методом систему линейных дифференциальных уравнений
Функции f1(t), f2(t) и значения ak, bk, ck, dk (k=1, 2), A, B, x(0), y(0) взять из табл. 16.5
2.25. a1 = 4, b1 = 1, c1 = 3, d1 = 0, f1(t) = 0, a2 = 1, b2 = 3, c2 = 0, d2 = 2, f2(t) = 1, x(0) = 0, y(0)=0